What is Mathematics?

                            गणित क्या है?
   गणित एक, पुराने व्यापक और गहरी अनुशासन (अध्ययन के क्षेत्र) है। गणित की शिक्षा में सुधार के लिए काम कर रहे लोगों को समझने की जरूरत है "गणित क्या है?"
                         A Tidbit of History
   शिक्षण और सीखने के लिए एक औपचारिक क्षेत्र के रूप में गणित सुमेर निवासी द्वारा करीब 5,000 साल पहले विकसित किया गया था।
मानव ज्ञान की कुछ प्राथमिक विधाओं में संभवतया गणित भी आता है और यह मानव सभ्यता जितना ही पुराना है। मानव जीवन के विस्तार और इसमें जटिलताओं में वृद्धि के साथ गणित का भी विस्तार हुआ है और उसकी जटिलताएं भी बढ़ी हैं। सभ्यता के इतिहास के पूरे दौर में गुफा में रहने वाले मानव के सरल जीवन से लेकर आधुनिक काल के घोर जटिल एवं बहुआयामी मनुष्य तक आते-आते मानव जीवन में धीरे-धीरे परिवर्तन आया है। इसके साथ ही मानव ज्ञान-विज्ञान की एक व्यापक एवं समृद्ध शाखा के रूप में गणित का विकास भी हुआ है। हालांकि एक आम आदमी को एक हजार साल से बहुत अधिक पीछे के गणित के इतिहास से उतना सरोकार नहीं होना चाहिए, परंतु वैज्ञानिक, गणितज्ञ, प्रौद्योगिकीविद्, अर्थशास्त्री एवं कई अन्य विशेषज्ञ रोजमर्रा के जीवन में गणित की समुन्नत प्रणालियों का किसी न किसी रूप में एक विशाल, अकल्पनीय पैमाने पर इस्तेमाल करते हैं। आजकल गणित दैनिक जीवन के साथ सर्वव्यापी रूप में समाया हुआ दिखता है।
गणित की उत्पत्ति कैसे हुई, यह आज इतिहास के पन्नों में ही विस्मृत है। मगर हमें मालूम है कि आज के 4000 वर्ष पहले बेबीलोन तथा मिस्र सभ्यताएं गणित का इस्तेमाल पंचांग (कैलेंडर) बनाने के लिए किया करती थीं जिससे उन्हें पूर्व जानकारी रहती थी कि कब फसल की बुआई की जानी चाहिए या कब नील नदी में बाढ़ आएगी, या फिर इसका प्रयोग वे वर्ग समीकरणों को हल करने के लिए किया करती थीं। उन्हें तो उस प्रमेय (थ्योरम) तक के बारे में जानकारी थी जिसका कि गलत श्रेय पाइथागोरस को दिया जाता है। उनकी संस्कृतियाँ कृषि पर आधारित थीं और उन्हें सितारों और ग्रहों के पथों के शुद्ध आलेखन और सर्वेक्षण के लिए सही तरीकों के ज्ञान की जरूरत थी। अंकगणित का प्रयोग व्यापार में रुपयों-पैसों और वस्तुओं के विनिमय या हिसाब-किताब रखने के लिए किया जाता था। ज्यामिति का इस्तेमाल खेतों के चारों तरफ की सीमाओं के निर्धारण तथा पिरामिड जैसे स्मारकों के निर्माण में होता था।

म्यान संख्या

मिलेटस निवासी थेल्स (645-546 ईसा पूर्व) को ही सबसे पहला सैद्धांतिक गणितज्ञ माना जाता है। उसने बताया कि किसी भी वस्तु की ऊंचाई को मापन छड़ी द्वारा निक्षेपित परछाई से तुलना करके मापा जा सकता है। ऐसा मानते हैं कि उसने एक सूर्य ग्रहण के होने के बारे में भी भविष्यवाणी की थी। उसके शिष्य पाइथागोरस ने ज्यामिति को यूनानियों के बीच एक मान्य विज्ञान का स्वरूप दिलाकर यूक्लिड और आर्किमिडीज के लिए आगे का मार्ग प्रशस्त किया।
बेबीलोन निवासियों के विरासत में मिले ज्ञान में यूनानियों ने काफी वृद्धि की। इसके अलावा गणित को एक तर्कसंगत पद्धति के रूप में उन्होंने स्थापित भी किया-एक ऐसी पद्धति जिसमें कुछ मूल तथ्यों या धारणाओं को सत्य मानकर (जिन्हें प्रमेय कहते हैं) निष्कर्षों (जिन्हें उपपत्ति या प्रमाण कहते हैं) तक पहुंचा जाता है।
भारत के लिये यह गौरव की बात है कि बारहवीं सदी तक गणित की सम्पूर्ण विकास-यात्रा में उसके उन्नयन के लिए किए गये सारे महत्वपूर्ण प्रयास अधिकांशतया भारतीय गणितज्ञों की खोजों पर ही आधारित थे।

                      एक विषय के रूप में गणित
   A discipline (a organized, formal field of study) such as mathematics tends to be defined by the types of problems it addresses, the methods it uses to address these problems, and the results it has achieved. 

पुरातन काल से ही सभी प्रकार के ज्ञान-विज्ञान में गणित का स्थान सर्वोपरि रहा है-

यथा शिखा मयूराणां नागानां मणयो यथा।

तथा वेदाङ्गशास्त्राणां गणितं मूर्ध्नि स्थितम्॥ (वेदांग ज्योतिष)

( जिस प्रकार मोरों में शिखा और नागों में मणि का स्थान सबसे उपर है, उसी प्रकार सभी वेदांग और शास्त्रों मे गणित का स्थान सबसे ऊपर है।)
महान गणितज्ञ गाउस ने कहा था कि गणित सभी विज्ञानों की रानी है। गणित, विज्ञान और प्रौद्योगिकी का एक महत्वपूर्ण उपकरण (टूल) है। भौतिकी, रसायन विज्ञान, खगोल विज्ञान आदि गणित के बिना नहीं समझे जा सकते। ऐतिहासिक रूप से देखा जाय तो वास्तव में गणित की अनेक शाखाओं का विकास ही इसलिये किया गया कि प्राकृतिक विज्ञान में इसकी आवश्यकता आ पड़ी थी।
कुछ हद तक हम सब के सब गणितज्ञ हैं। अपने दैनिक जीवन में रोजाना ही हम गणित का इस्तेमाल करते हैं - उस वक्त जब समय जानने के लिए हम घड़ी देखते हैं, अपने खरीदे गए सामान या खरीदारी के बाद बचने वाली रेजगारी का हिसाब जोड़ते हैं या फिर फुटबाल टेनिस या क्रिकेट खेलते समय बनने वाले स्कोर का लेखा-जोखा रखते हैं।
व्यवसाय और उद्योगों से जुड़ी लेखा संबंधी संक्रियाएं गणित पर ही आधारित हैं। बीमा (इंश्योरेंस) संबंधी गणनाएं तो अधिकांशतया ब्याज की चक्रवृद्धि दर पर ही निर्भर है। जलयान या विमान का चालक मार्ग के दिशा-निर्धारण के लिए ज्यामिति का प्रयोग करता है। भौगोलिक सर्वेक्षण का तो अधिकांश कार्य ही त्रिकोणमिति पर आधारित होता है। यहां तक कि किसी चित्रकार के आरेखण कार्य में भी गणित मददगार होता है, जैसे कि संदर्भ (पर्सपेक्टिव) में जिसमें कि चित्रकार को त्रिविमीय दुनिया में जिस तरह से इंसान और वस्तुएं असल में दिखाई पड़ते हैं, उन्हीं का तदनुरूप चित्रण वह समतल धरातल पर करता है।
संगीत में स्वरग्राम तथा संनादी (हार्मोनी) और प्रतिबिंदु (काउंटरपाइंट) के सिद्धांत गणित पर ही आश्रित होते हैं। गणित का विज्ञान में इतना महत्व है तथा विज्ञान की इतनी शाखाओं में इसकी उपयोगिता है कि गणितज्ञ एरिक टेम्पल बेल ने इसे ‘विज्ञान की साम्राज्ञी और सेविका’ की संज्ञा दी है। किसी भौतिकविज्ञानी के लिए अनुमापन तथा गणित का विभिन्न तरीकों का बड़ा महत्व होता है। रसायनविज्ञानी किसी वस्तु की अम्लीयता को सूचित करने वाले पी एच (pH) मान के आकलन के लिए लघुगणक का इस्तेमाल करते हैं। कोणों और क्षेत्रफलों के अनुमापन द्वारा ही खगोलविज्ञानी सूर्य, तारों, चंद्र और ग्रहों आदि की गति की गणना करते हैं। प्राणी-विज्ञान में कुछ जीव-जन्तुओं के वृद्धि-पैटर्नों के विश्लेषण के लिए विमीय विश्लेषण की मदद ली जाती है।
उच्च गतिवाले संगणकों द्वारा गणनाओं को दूसरी विधियों द्वारा की गई गणनाओं की अपेक्षा एक अंश मात्र समय के अंदर ही सम्पन्न किया जा सकता है। इस तरह कम्यूटरों के आविष्कार ने उन सभी प्रकार की गणनाओं में क्रांति ला दी है जहां गणित उपयोगी हो सकता है। जैसे-जैसे खगोलीय तथा काल मापन संबंधी गणनाओं की प्रामाणिकता में वृद्धि होती गई, वैसे-वैसे नौसंचालन भी आसान होता गया तथा क्रिस्टोफर कोलम्बस और उसके परवर्ती काल से मानव सुदूरगामी नए प्रदेशों की खोज में घर से निकल पड़ा। साथ ही, आगे के मार्ग का नक्शा भी वह बनाता गया। गणित का उपयोग बेहतर किस्म के समुद्री जहाज, रेल के इंजन, मोटर कारों से लेकर हवाई जहाजों के निर्माण तक में हुआ है। राडार प्रणालियों की अभिकल्पना तथा चांद और ग्रहों आदि तक राकेट यान भेजने में भी गणित से काम लिया गया है।
                                       
                                                         भौतिकी में गणित का महत्व

• विद्युतचुम्बकीय सिद्धान्त समझने एवं उसका उपयोग करने के लिये के लिये सदिश विश्लेषण बहुत महत्वपूर्ण है।

• ग्रुप सिद्धान्त, स्पेक्ट्रोस्कोपी, क्वांटम यांत्रिकी, ठोस अवस्था भौतिकी एवं नाभिकीय भौतिकी के लिये बहुत उपयोगी है।

• भौतिकी में सभी तरह के रेखीय संकायों के विश्लेषण के लिये फुरिअर की युक्तियाँ उपयोगी है।

• क्वान्टम् यान्त्रिकी को समझने के लिये मैट्रिक्स विश्लेषण जरूरी है।

• विद्युतचुम्बकीय तरंगों का वर्णन करने एवं क्वान्टम यांत्रिकी के लिये समिश्र संख्याओं का उपयोग होता है।

                                  गणित कार्यपद्धति

  गणित मानव मस्तिष्क की उपज है। मानव की गतिविधियों एवं प्रकृति के निरीक्षण द्वारा ही गणित का उद्भव हुआ। मानव मस्तिष्क की चिंतन प्रक्रियाओं के मूल में पैठ कर ही गणित मुखर रूप से उनकी अभिव्यक्ति करता है और वास्तविक संसार अवधारणाओं की दुनिया में बदल जाता है। गणित वास्तविक जगत को नियमित करने वाली मूर्त धारणाओं के पीछे काम करने वाले नियमों का अध्ययन करता है। ज्यादातर दैनिक जीवन का गणित इन मूल धारणाओं का ही सार है और इसलिए इसे आसानी से समझा-बूझा जा सकता है। हालांकि अधिकांश धारणाएं अंत:प्रज्ञा के द्वारा ही हम पर प्रकट होती है, फिर भी शुद्ध एवं संक्षेप रूप में उन धारणाओं को व्यक्त करने के लिए उचित शब्दावली एवं कुछ नियमों और प्रतीकों की आवश्यकता पड़ती है।
  अत: गणित की अपनी अलग ही भाषा एवं लिपि होती है जिसे पहले जानना-समझना जरूरी होता है। शायद यही कारण है कि दैनिक जीवन से असंबद्धित मानकर इसे समझने की दृष्टि से कठिन माना जाता है, जबकि हकीकत में यह वास्तविक जीवन के साथ अभिन्न रूप से जुड़ा ही नहीं है, बल्कि उसी से इसकी उत्पत्ति भी हुई है। यह विडंबना ही है कि ज्यादातर लोग गणित के प्रति विमुखता दिखा कर उससे दूर भागते हैं, जबकि वस्तुस्थिति यह है कि जीवन तथा ज्ञान के हर क्षेत्र में इसकी उपयोगिता है। यह केवल संयोग नहीं है कि आर्किमिडीज, न्यूटन(Newton), गौस और लैगरांज जैसे महान वैज्ञानिकों के विज्ञान के साथ-साथ गणित में भी अपना महान योगदान दिया है।
  

                           गणित का वर्गीकरण

  वर्तमान में गणित को मोटे तौर पर दो भागों में बांटा जाता है:
  
• अनुप्रयुक्त गणित या नियोज्य गणित (Applied Mathematics) और
• शुद्ध गणित (Pure Mathematics)।

            अनुप्रयुक्त गणित

  विज्ञान, अर्थशास्त्र और अन्य कई क्षेत्रों में प्रयोग किया जाने वाला गणित प्रायोगिक गणित है और इसमें अध्ययन की जाने वाली गणितीय समस्याओं का स्रोत किसी और क्षेत्र में होता है। इसके अन्तर्गत यंत्रशास्त्र, भूमापन, भूपदार्थ विज्ञान, ज्योतिष आदि विषय है।
  

  गणितीय भौतिकी	तरल गतिकी	इष्टतमकरण	प्रायिकता	सांख्यिकी	गणितीय वित्त	खेल सिद्धांत

             शुद्ध गणित

  शुद्ध गणित स्वयं गणित में उपजी उन समस्याओं का हल ढूंढता है जिनका अन्य क्षेत्रों से सीधा सम्बन्ध नहीं है। कई बार समय के साथ-साथ शुद्ध गणित के अनुप्रयोग मिलते जाते हैं और इस प्रकार उसका कुछ हिस्सा प्रायोगिक गणित में आता जाता है। शुद्ध गणित के अंतर्गत, बीजगणित, ज्यामिति और संख्या सिद्धांत आदि आते हैं। फ़रमा का सुप्रसिद्ध प्रमेय, संख्या सिद्धान्त का ही एक अंग है। शुद्ध गणित का विकास बीसवीं शताब्दी में बहुत अधिक हुआ और इसके विकास में १९०० में डेविड हिल्बर्ट के द्वारा पेरिस में दिये गये व्याख्यान का बहुत योगदान रहा।
  

                                                                        संख्याएँ

  ${\displaystyle 1,2,3,\ldots \!}$	${\displaystyle \ldots ,-2,-1,0,1,2\,\ldots \!}$	${\displaystyle -2,{\frac {2}{3}},1.21\,\!}$	${\displaystyle -e,{\sqrt {2}},3,\pi \,\!}$	${\displaystyle 2,i,-2+3i,2e^{i{\frac {4\pi }{3}}}\,\!}$
  प्राकृतिक संख्याएँ	पूर्णांक	परिमेय संख्याएँ	वास्तविक संख्याएँ	समिश्र संख्याएँ

         

                                                                        संरचनाएँ (structures)

${\displaystyle {\begin{matrix}(1,2,3)&(1,3,2)\\(2,1,3)&(2,3,1)\\(3,1,2)&(3,2,1)\end{matrix}}}$
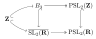
सांयोगिकी	संख्या सिद्धान्त	समूह सिद्धांत	ग्राफ सिद्धान्त	क्रम सिद्धान्त (Order theory)	बीजगणित

आकाश (space)

ज्यामिति	त्रिकोणमिति	अवकल ज्यामिति	टोपोलोजी	फ्रैक्टल ज्यामिति	मापन सिद्धान्त

रूपान्तरण (transformation)

कैलकुलस	सदिश कैलकुलस	अवकल समीकरण	गतीय निकाय	अक्रम सिद्धान्त (chaos theory)	समिश्र विश्लेषण

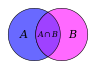
विविक्त गणित (Discrete mathematics)

सैद्धान्तिक संगणक विज्ञान में काम आने वाले गणित का सामान्य नाम विविक्त गणित है। इसमें संगणन सिद्धान्त (Theory of Computation), संगणनात्मक जटिलता सिद्धान्त, तथा सैधान्तिक कम्प्यूतर विज्ञान शामिल हैं।

${\displaystyle {\begin{matrix}\left[1,2,3\right]&\left[1,3,2\right]\\\left[2,1,3\right]&\left[2,3,1\right]\\\left[3,1,2\right]&\left[3,2,1\right]\end{matrix}}}$
सांयोजिकी	सहज कुलक सिद्धांत	संगणन सिद्धान्त	कूटन (Encryption)	ग्राफ सिद्धान्त

संगणन के उपकरण

नीचे कुछ मुक्तस्रोत कम्प्यूटर सॉफ्टवेयरों का नाम दिया गया है जो गणित के विभिन्न कार्य करने के लिए बहुत उपयोगी हैं।

	मैक्सिमा (Maxima (software))	http://maxima.sourceforge.net/
110px	साईलैब (Scilab)	http://scilabsoft.inria.fr/
	आर (सोफ्टवेयर) (R (software))	http://www.r-project.org/
	GNU आक्टेव	http://www.octave.org

प्रमुख गणितज्ञ

• 

  अल्-ख्वारिज्मी^[1]
• 

  डी'एलम्बर्ट^[2]
• 

  आर्कीमीडीज^[3]
• 

  जॉर्ज बूल
• 

  जॉर्ज कैण्टर
• 

  Cauchy(कउची )
• 

  Richard Dedekind (रिचर्ड दडकिंद )
• 

  रेने देकार्तीज
• 

  Euclides(उक्लिदेस )
• 

  लियोनार्ड आयलर
• 

  पियरे डी फर्मा
• 

  Galois
• 

  कार्ल फ्रेडरिक गाउस
• 

  गोडेल्
• 

  हैमिल्टन
• 

  हिल्बर्ट
• 

  Hipátia
• 

  जैकोबी
• 

  ओमर खैयाम
• 

  Klein
• 

  कोल्मोगोरोव
• 

  लाग्रेंज
• 

  पियरे साइमन लाप्लास
• 

  लैब्नीज
• 

  Lebesgue
• 

  Nash
• 

  जॉन फॉन न्युमान
• 

  आइजक न्यूटन
• 

  Noether
• 

  पास्कल
• 

  Peano
• 

  पाइथागोरस
• 

  Poincaré
• 

  Pontryagin
• 

  श्रीनिवास रामानुजन
• 

  Riemann
• 

  बर्ट्राण्ड रसेल
• 

  Steiner
• 

  Weyl
• 

  Zermelo